柤屆壆戝妛俀侽俀俆擭棟宯悢妛戞係栤丒暥宯悢妛戞俁栤乮栤戣乯
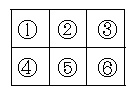
丂僐僀儞嘆丄乧丄嘐偑壓恾偺傛偆偵儅僗栚偺拞偵抲偐傟偰偄傞丅
丂
丂偙傟傜偺僐僀儞偐傜柍嶌堊偵傂偲偮傪慖傃丄慖傫偩僐僀儞偼偦偺傑傑偵偟丄偦偺僐僀儞偺偁傞儅僗栚偲曈傪嫟桳偟偰椬愙偡傞儅僗栚偺僐僀儞傪棤曉偡憖嶌傪峫偊傞丅椺偊偽丄嘆傪慖傋偽丄嘇丄嘋傪棤曉偟丄嘇傪慖傋偽丄嘆丄嘊丄嘍傪棤曉偡丅嵟弶偼偡傋偰偺僐僀儞偑昞岦偒偵抲偐傟偰偄偨偲偡傞丅惓偺惍悢値偵懳偟丄値夞栚偺偺憖嶌廔椆帪揰偱偡傋偰偺僐僀儞偑棤岦偒偱偁傞妋棪傪pn偲偡傞偲偒丄埲壓偺栤偵摎偊傛丅
乮侾乯p2傪媮傔傛丅
乮俀乯僐僀儞嘆丄乧丄嘐傪僌儖乕僾俙丄俛偵暘偗傞偙偲偵傛偭偰丄値夞栚偺憖嶌廔椆帪揰偱偡傋偰偺僐僀儞偑棤岦偒偱偁傞偨傔偺昁梫廫暘忦審傪師偺宍偵昞偡偙偲偑偱偒傞丅
丂値夞栚偺憖嶌廔椆帪揰傑偱偵俙偵懏偡傞奺僐僀儞偼偦傟偧傟婏悢夞慖偽傟丄俛偵懏偡傞奺僐僀儞偼偦傟偧傟嬼悢夞慖偽傟傞丅
丂偳偺傛偆偵僌儖乕僾暘偗偡傟偽傛偄偐摎偊傛丅
乮俁乯p4傪媮傔傛丅
乮拲乯
妋棪仺彫妛惗偺応崌丄偲傝偁偊偢丄偡傋偰偺応崌偵懳偟偰偁傞応崌偑婲偙傞妱崌偲峫偊傟偽傛偄偱偟傚偆丅
惓偺仺侽傛傝戝偒偄
乮俀乯偺栤戣暥偑彫妛惗偵偼傢偐傝偵偔偄偱偡偑丄梫偡傞偵丄僐僀儞嘆丄乧丄嘐傪偦傟偧傟慖傫偩夞悢偼婏悢夞偐嬼悢夞偐摎偊側偝偄偲偄偆偙偲偱偡丅乮俁乯傪夝偔偨傔偺僸儞僩偵夁偓側偄偺偱丄彫妛惗偺応崌柍帇偟偰傕傛偄偱偟傚偆丅乮俁乯傪夝偙偆偲偡傟偽丄偙偺偙偲傪峫偊傞偙偲偵側傝傑偡偐傜偹丅