柤屆壆戝妛俀侽俀俆擭棟宯悢妛戞係栤丒暥宯悢妛戞俁栤乮夝摎丒夝愢乯
乮侾乯
嘇丄嘐傪慖傇偲僐僀儞傪俁枃棤曉偡偙偲偵側傝丄偦傟埲奜偺僐僀儞傪慖傇偲僐僀儞傪俀枃棤曉偡偙偲偵側傞偐傜丄俀夞偱俇枃偺僐僀儞傪棤曉偡偨傔偵偼丄嘇偲嘐偺僐僀儞傪侾夞偢偮慖傇偙偲偵側傝傑偡丅
俀夞偺憖嶌偱偺僐僀儞偺慖傃曽偼慡晹偱乮俇亊俇乯捠傝偁傝丄偦偺偆偪忦審傪枮偨偡僐僀儞偺慖傃曽偼丄嘇仺嘐傑偨偼嘐仺嘇偺俀捠傝偁傞偐傜丄媮傔傞妋棪偼俀/乮俇亊俇乯亖侾/侾俉偲側傝傑偡丅
乮俀乯
拞妛擖帋偵傕摨偠傛偆側栤戣偑弌偝傟偰偄傑偡乮乮儔丒僒乕儖拞妛峑侾俋俋係擭嶼悢俀擔栚戞俁栤丄宑滀媊弇拞摍晹俀侽侾俇擭嶼悢戞俈栤側偳乯丅
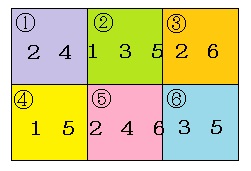
奺僐僀儞偑抲偐傟偨偲偙傠偵丄偳偺僐僀儞傪慖傫偩偲偒偵棤曉偝傟傞偐傪恾偺傛偆偵乮懢帤偱乯彂偒崬傒傑偡丅丂仼奺僐僀儞偑抲偐傟偨偲偙傠偲椬傝崌偆偲偙傠偺僐僀儞偺斣崋傪彂偔偩偗偺婡夿揑側嶌嬈偱偡丅
丂
忦審傛傝丄偦傟偧傟偺僐僀儞偑婏悢夞棤曉偝傟傞偙偲偵側傞偐傜丄奺僐僀儞偑抲偐傟偨偲偙傠偵彂偄偨僐僀儞偑慖偽傟偨崌寁夞悢偼婏悢偲側傝傑偡乮椺偊偽丄僐僀儞嘋偑抲偐傟偨偲偙傠偵彂偄偨僐僀儞乮僐僀儞嘆偲僐僀儞嘍乯偑慖偽傟偨崌寁夞悢偼婏悢偲側傝傑偡偹乯丅丂仼嬼婏惈偵拝栚偡傞偙偲偑栤戣暥偱帵嵈偝傟偰偄傑偡偑丄偪傚偭偲峫偊傟偽傢偐傞偙偲偱偡偹丅
墿怓偺晹暘偲墿椢怓偺晹暘傪斾傋傞偲丄嘊偺僐僀儞偼嬼悢夞棤曉偝傟偨偙偲偵側傝丄悈怓偺晹暘偐傜丄嘍偺僐僀儞偼婏悢夞棤曉偝傟偨偙偲偵側傝丄墿怓偺晹暘偐傜丄嘆偺僐僀儞偼嬼悢夞棤曉偝傟偨偙偲偵側傝傑偡丅
偙偺偲偒丄墿怓偺晹暘丄墿椢怓偺晹暘丄悈怓偺晹暘偼偡傋偰婏悢夞棤曉偝傟傞偙偲偵側傝傑偡偹丅
巆傝偺晹暘偵偮偄偰摨條偺嶌嬈傪峴偆偲丄嘐偺僐僀儞偑嬼悢夞丄嘇偺僐僀儞偑婏悢夞丄嘋偺僐僀儞偑嬼悢夞棤曉偝傟傞偙偲偵側傝傑偡丅
偟偨偑偭偰丄俙偵懏偡傞僐僀儞偼嘇偲嘍偲側傝丄俛偵懏偡傞僐僀儞偼嘆偲嘊偲嘋偲嘐偲側傝傑偡丅
乮俁乯
慡晹偱係夞僐僀儞傪慖傇偙偲偵側傝傑偡偹丅
僐僀儞傪慖傇僷僞乕儞偼師偺俁偮偺応崌偵側傝傑偡丅
乮偁乯僐僀儞嘇偲僐僀儞嘍傪侾夞偢偮丄僐僀儞嘆偲嘊偲嘋偲嘐偺偆偪偄偢傟偐侾枃偺僐僀儞傪俀夞慖傃丄巆傝偺僐僀儞傪慖偽側偄応崌
乮偄乯僐僀儞嘇傪侾夞偲僐僀儞嘍傪俁夞慖傃丄巆傝偺僐僀儞傪慖偽側偄応崌
乮偆乯僐僀儞嘇傪俁夞偲僐僀儞嘍傪侾夞慖傃丄巆傝偺僐僀儞傪慖偽側偄応崌
乮偁乯偺応崌
僐僀儞嘆偲嘊偲嘋偲嘐偺偆偪偳偺僐僀儞傪俀夞慖傇偐偱係捠傝偁傝丄偦偺偦傟偧傟偵懳偟偰丄僐僀儞嘇偑壗夞栚偵弌傞偐偱係捠傝偁傝丄偦偺偦傟偧傟偵懳偟偰丄僐僀儞嘍偑壗夞栚弌偱傞偐傜偱俁捠傝偁傞偐傜丄偙偺応崌偼慡晹偱係亊係亊俁亖係俉捠傝偁傝傑偡丅
乮偄乯偺応崌
僐僀儞嘇傪壗夞栚偵慖傇偐偱係捠傝偁傝傑偡丅
乮偆乯偺応崌
乮偄乯偺応崌摨條丄係捠傝偁傝傑偡丅丂仼忦審偺懳摍惈傪棙梡偟偰嶌嬈傪尭傜偡両
係夞偺憖嶌偱偺僐僀儞偺慖傃曽偼慡晹偱乮俇亊俇亊俇亊俇乯捠傝偁傞偐傜丄媮傔傞妋棪偼
丂丂乮係俉亄係亄係乯/乮俇亊俇亊俇亊俇乯
丂亖俈/侾俇俀
偲側傝傑偡丅