東京大学2024年文科数学第4問(解答・解説)
n=5のときは、4頂点をどのように選んでも条件を満たすので、確率は1となります。 ←100%ということですね。
以下、nが7以上の奇数の場合について考えます。
四角形ABCDの内部にOが含まれないものを数えることにします。
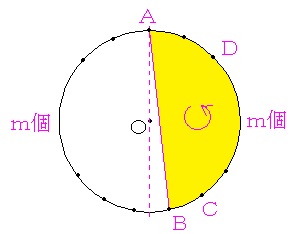
四角形の4頂点を反時計回りにA、B、C、Dとし、四角形の辺のうちOに最も近いものを辺ABとします。 ←ダブりを防ぐためです。このようにすることで、図の黄色の部分に四角形を配置することになります。
点Aの選び方はn通りあります。
nを2×m+1(mは3以上の整数)とし、A以外の残り3つの頂点を選びます。
Aに決まった頂点以外の残りの2×m個の頂点を正n角形の線対称の軸によってm個ずつ分けます。
四角形ABCDの内部にOが含まれないのは、図の黄色の部分(Aは除きます)のm個の頂点から3個の頂点を選んで、反時計回りにB、C、Dとしたときになります。
四角形ABCDの内部にOが含まれない場合は
n×m×(m−1)×(m−2)/(3×2×1) ←組合せですね。
=n×(n−1)/2×(n−3)/2×(n−5)/2×1/(3×2×1) ←n=2×m+1を逆算して、m=(n−1)/2となることを利用しました。
=n×(n−1)×(n−3)×(n−5)/(2×4×3×2×1)通り
あります。
また、四角形の4頂点の選び方は全部で
n×(n−1)×(n−2)×(n−3)/(4×3×2×1) ←組合せですね。
=2×n×(n−1)×(n−2)×(n−3)/(2×4×3×2×1)通り ←比率をわかりやすくするために、このように変形しました。
あるから、四角形ABCDの内部にOが含まれない確率は(n−5)/{2(n−2)}となり、求める確率は、
1−(n−5)/{2(n−2)} ←すべての確率から条件を満たさない場合の確率を引きます。
={2×(n−2)−(nー5)}/{2(n−2)}
=(2×n−4+5−n)/{2(n−2)} ←分子の計算は小学生にはやや難しいかもしれませんね。2×(n−2)−(nー5)の引かれる数と引く数の両方に5を足しました(差一定)。その後、2×(n−2)については分配法則を利用しました。
=(n+1)/{2(n−2)}
となり、これはnが5のときも成り立ちますね。
一橋大学で三角形の場合の問題(一橋大学2024年数学第5問)が出されていて、上の解説と同様の考え方で鈍角三角形を数えることができます。
三角形の3頂点を反時計回りにA、B、Cとし、三角形の辺のうちOに最も近いものを辺ABとします。
鈍角三角形はn×m×(m−1)/(2×1)通り(n=2×m+1)、三角形は全部でn×(n−1)×(n−2)/(3×2×1)通りとなります。