九州大学2000年後期理系数学第4問(2)(解答・解説)
有名問題(フロベニウスの硬貨交換問題(シルベスターの切手問題))で、5円切手と6円切手の組合せでは作ることができない最大の金額は5×6−(5+6)=19円となります。
この知識により証明終わりというのは、さすがにやばいでしょう。
さて、問題を解いてみましょう。
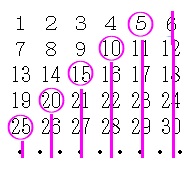
まず、1から30までの30個の数字を並べます。
その際、横に6個並べます。
右端の数は6の倍数だからすべて作ることができますね。
次に、5の倍数に〇をつけます。 ←横に6個ずつ数字を並べているので、左斜め下方向に現れます。
〇の下の数字は6を順次足していくことにより、すべて作ることができます。
したがって、20円以上の任意の値段分の切手は5円切手と6円切手の組合せとして買えることになります。
大学入試であれば、6×□(6の倍数、□=1、2、3、・・・)、5+6×〇(6で割ると5余る数、〇=0、1、2、・・・)、10+6×△=4+6+6×△(6で割ると4余る数(10以上のもの)、△=0、1、2、・・・)、・・・、25+6×☆=1+6×4+6×☆(6で割ると1余る数(25以上)、☆=0、1、2、・・・)がすべて表すことができると書けばいいだけの話ですね。
因みに、日本数学オリンピック(JMO)と阪大で同じような問題が出されています(日本数学オリンピック2000年予選第2問、大阪大学2000年前期理系数学第3問)し、中学入試でも同じような問題(甲陽学院中学校1997年算数2日目第3問、甲南中学校2000年算数2期第3問、渋谷教育学園幕張中学校2013年算数第3問など)が出されています。