ラ・サール中学校2004年算数第4問(解答・解説)
メインの(3)を解いてしまいます。
2色以下で塗ることはできませんね。
赤、青、黄をそれぞれを〇、△、□とします。
AからEまで順に色を塗っていくとき、〇の次は△または□、△の次は〇または□、□の次は〇または△を塗ることになりますが、最初(A)と最後(E)は違う色を塗ることに注意が必要です。
〇→△ △→〇 □→〇
→□ →□ →△
逆から考えると、
〇の個数=1つ前の△の個数+1つ前の□の個数
△の個数=1つ前の□の個数+1つ前の〇の個数
□の個数=1つ前の〇の個数+1つ前の△の個数
となることがわかるので、機械的に処理できます。
まず、最初が〇の場合について考えると、以下の表のように、条件を満たすものは5×2=10通りあります。最初が△、□の場合も同じだから、求める塗り方はは10×3=30通りとなります。 ←〇と△と□は条件的に同じだからです。〜条件の対等性を利用して作業を減らす!
A B C D E
〇 1 0 2 2 6
△ 0 1 1 3 5
□ 0 1 1 3 5
ホームページで、この問題と同様の解法で解ける問題を取り上げているので、ぜひ解いてみましょう(京都大学1999年前期文系数学第5問、大阪星光学院中学校2007年算数第4問、灘中学校1996年算数1日目第9問、ラ・サール中学校1997年算数1日目第4問など)。
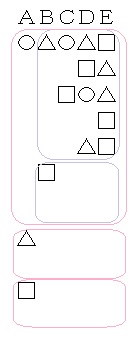
なお、条件の対等性を駆使しながら、樹形図をかいて解くこともできます(図の同じ色で囲んだ部分が条件的に同じ部分になります)。
1分もかかりませんよ。
さて、(1)と(2)を処理しておきましょう。
(1)
Aを考慮する必要はありません。
Bが△、Eが□だから、(C,D)=(〇,△)、(□,〇)、(□,△)の3通りあります。
(2)
Aを考慮する必要はありません。
BとEが△だから、(C,D)=(〇,□)、(□,〇)の2通りあります。
(1)、(2)をそれぞれ一般化すると、(1)はA、B、Eで3色使った場合となり、(2)はA、B、Eで2色だけ使った場合となります。
したがって、3×2×1×((1)の答え)+3×2×((2)の答え)とすれば、(3)の答えが求められます。